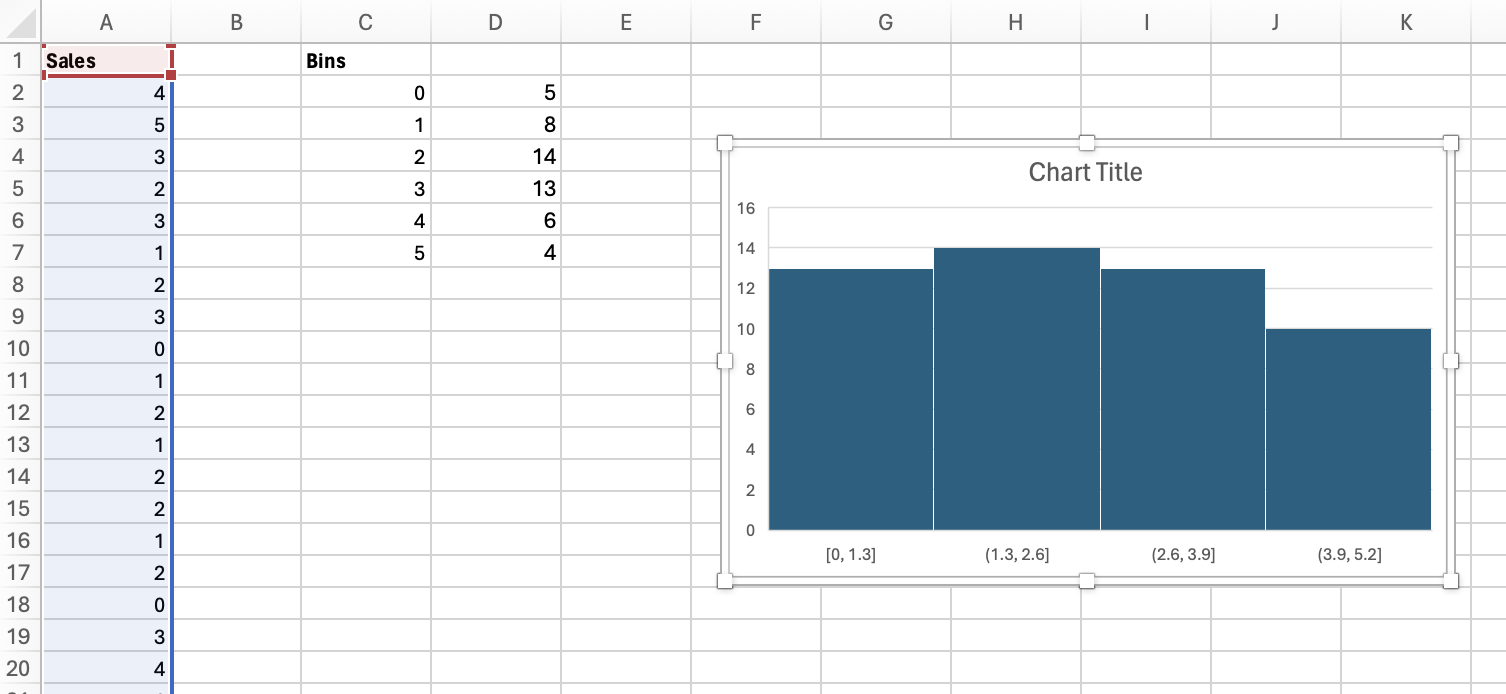
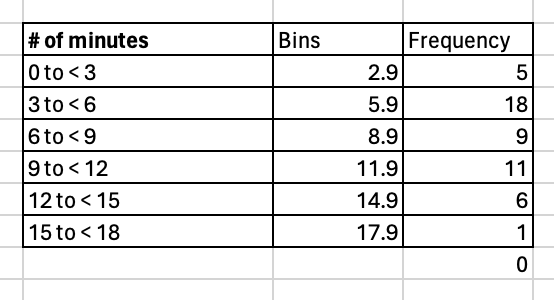
Definition 2.1.1.
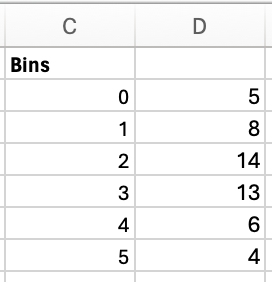
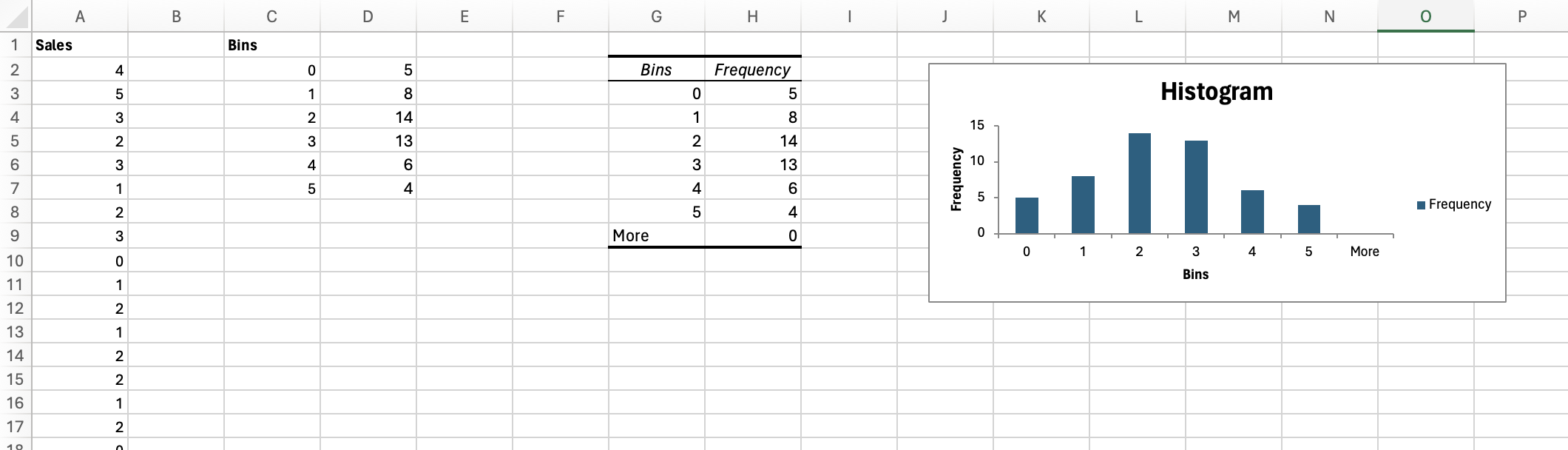
- frequency distribution: a table that shows the number of data observations that fall into specific intervals or categories
- class: a category in a frequency distribution
- relative frequency distribution: displays the proportion of observations of each class relative to the total number of observations
- cumulative frequency distribution: totals the proportion of observations that are less than or equal to the class at which you are looking