Section Quiz 4 Example Problems
Below are example problems for Quiz 4.
-
Objective 4a Example Problem:
Example 1.3. Objective 4a Example Problem.
Your class conducted a survey last week on whether students prefer digital or paper textbooks. Out of 120 responses, 72 preferred digital.
You are designing a promotional campaign for a new digital textbook. You plan to randomly sample 10 students from the same population.
-
Assuming it is appropriate to model the number of students who prefer digital textbooks using a binomial distribution, what formula would you use to find the probability that less than 8 of the 10 sampled students prefer digital?
Options:
1-BINOM.DIST(7,10,72/120,0)
1-BINOM.DIST(8,10,72/120,1)
1-BINOM.DIST(7,10,72/120,1)
BINOM.DIST(7,10,72/120,1)
BINOM.DIST(8,10,72/120,1)
BINOM.DIST(8,10,72/120,0)
1-BINOM.DIST(8,10,72/120,0)
1-NORM.DIST(8,10,72/120,1)
NORM.DIST(8,10,72/120,1)
-
Assuming it is appropriate to model the number of students who prefer digital textbooks using a binomial distribution, what formula would you use to find the probability that at least 8 of the 10 sampled students prefer digital?
Options:
1-BINOM.DIST(7,10,72/120,0)
1-BINOM.DIST(8,10,72/120,1)
1-BINOM.DIST(7,10,72/120,1)
BINOM.DIST(7,10,72/120,1)
BINOM.DIST(8,10,72/120,1)
BINOM.DIST(8,10,72/120,0)
1-BINOM.DIST(8,10,72/120,0)
1-NORM.DIST(8,10,72/120,1)
NORM.DIST(8,10,72/120,1)
-
Objective 4b Example Problem:
Example 1.4. Objective 4b Example Problem.
Let \(Z\) be the standard normal variable.
-
Consider the Excel formula given below:
\begin{equation*}
=1-NORM.S.DIST(1.06,1)
\end{equation*}
Which of the following probabilities could this formula be used to calculate?
Options:
the probability that Z is bigger than 1.06
the probability that Z is less than 1.06
the probability that Z is equal to 1.06
the probability that Z is between 1 and 1.06
-
Consider the Excel formula given below:
\begin{equation*}
=NORM.S.DIST(3.2,1)-NORM.S.DIST(-1.7,1)
\end{equation*}
Which of the following probabilities could this formula be used to calculate?
Options:
the probability that Z is between -1.7 and 3.2
the probability that Z is bigger than 3.2 or smaller than -1.7
the probability that Z is bigger than 3.2 and -1.7
the probability that Z is between 1 and 3.2 or between 1 and -1.7
-
Which of these formulas could be used to find \(z^{\star}\) such that \(P(Z\leq z^{\star})=0.96\text{?}\)
Options:
=NORM.S.INV(0.04)
=NORM.S.INV(0.96)
=NORM.S.DIST(0.96)
=NORM.S.DIST(0.04)
=1-NORM.S.INV(0.96)
=1-NORM.S.INV(0.04)
=1-NORM.S.DIST(0.96)
=1-NORM.S.DIST(0.04)
-
Which of these formulas could be used to find \(z^{\star}\) such that \(P(-z^{\star}\leq Z\leq z^{\star})=0.95\text{?}\)
-
Objective 4c Example Problem:
Example 1.5. Objective 4c Example Problem.
A random variable follows a normal probability distribution with a standard deviation of 5.
-
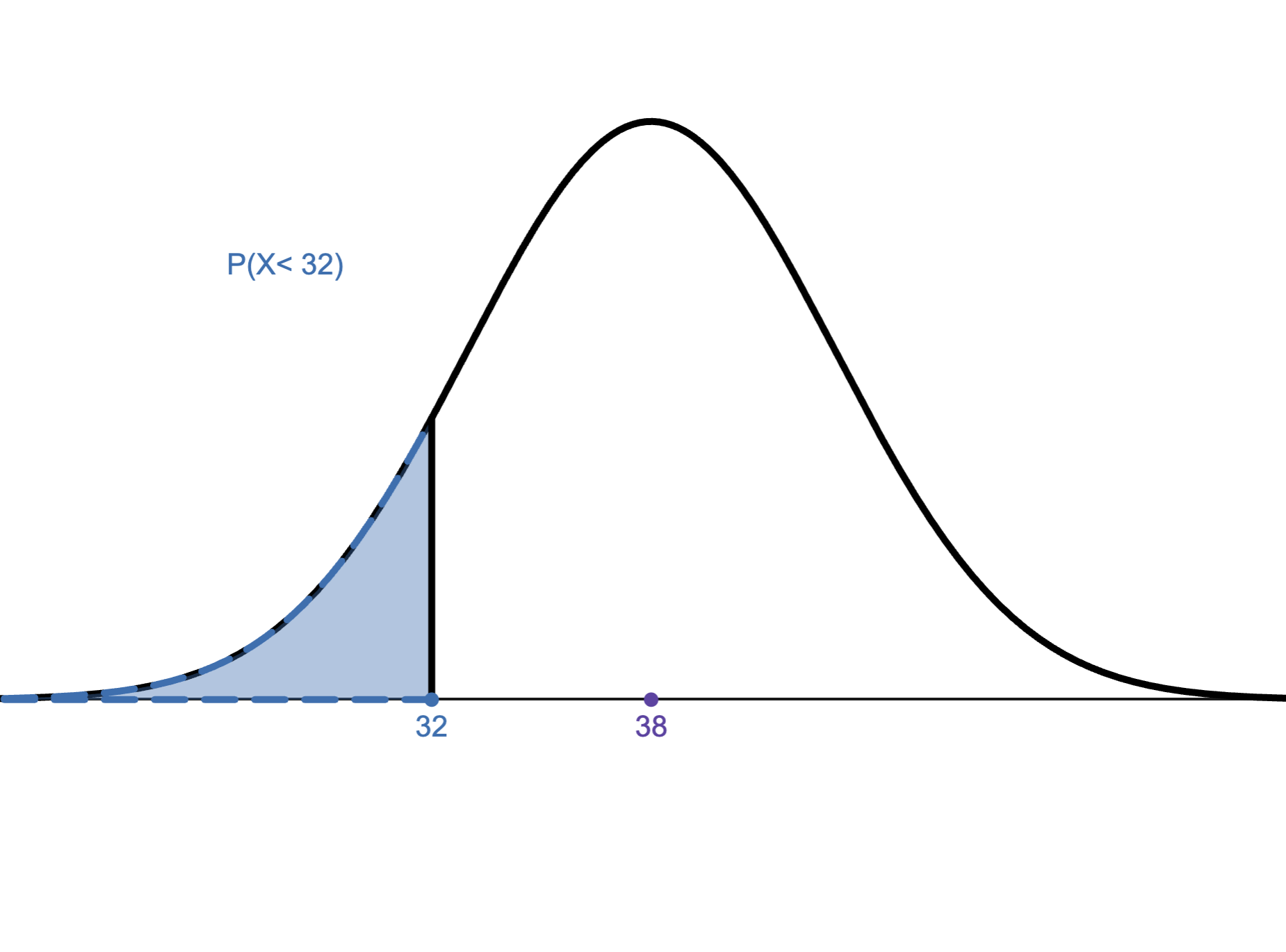
What formula would you use to find the probability shown below?
Options:
NORM.DIST(32,38,5,1)
1-NORM.DIST(32,38,5,1)
NORM.DIST(32,5,38,1)
1-NORM.DIST(32,5,38,1)
NORM.DIST(32,38,5,0)
1-NORM.DIST(32,38,5,0)
NORM.S.DIST(32,1)
1-NORM.S.DIST(32,1)
-
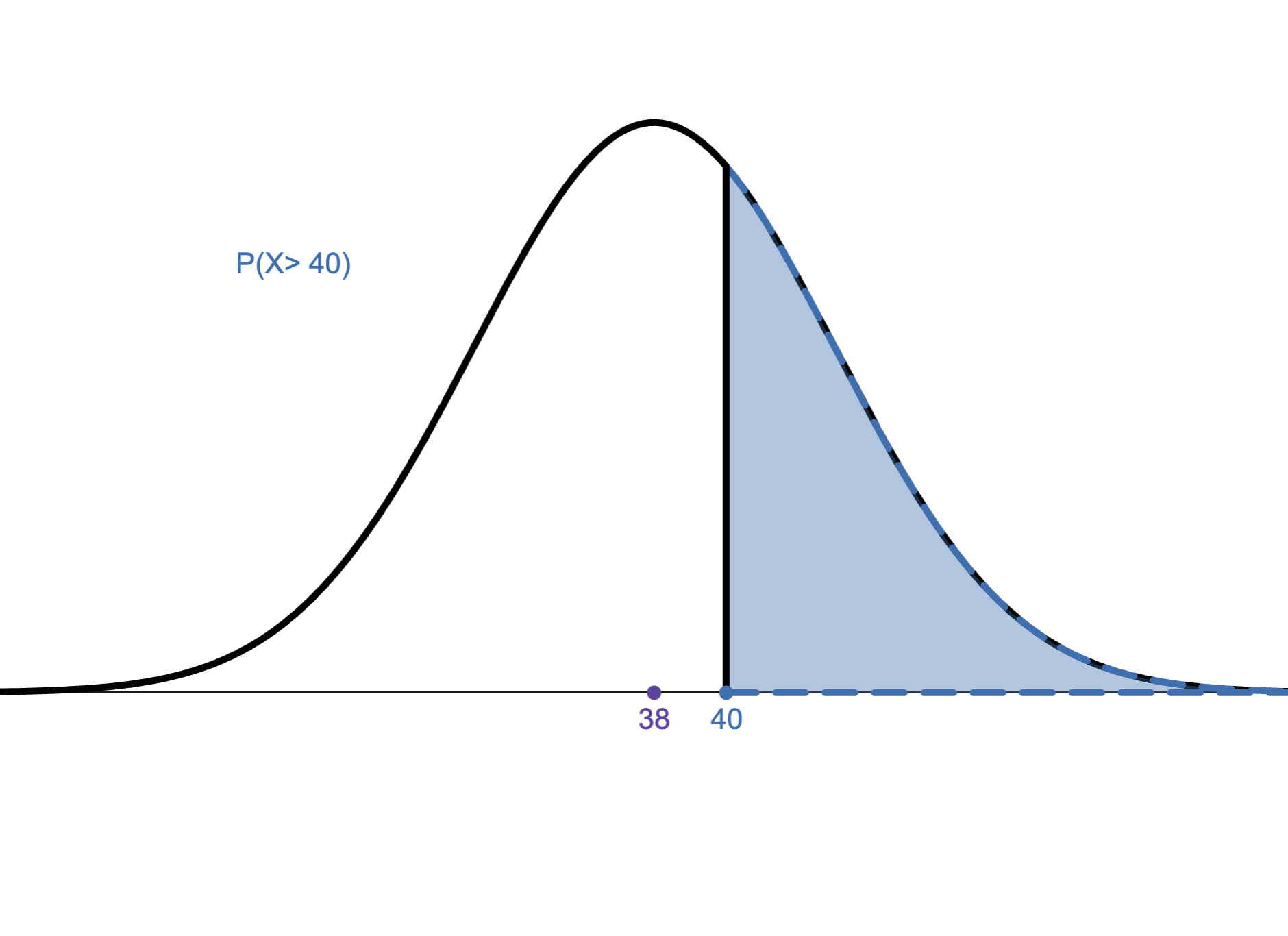
What formula would you use to find the probability shown below?
Options:
NORM.DIST(40,38,5,1)
1-NORM.DIST(40,38,5,1)
NORM.DIST(40,5,38,1)
1-NORM.DIST(40,5,38,1)
NORM.DIST(40,38,5,0)
1-NORM.DIST(40,38,5,0)
NORM.S.DIST(40,1)
1-NORM.S.DIST(40,1)
-
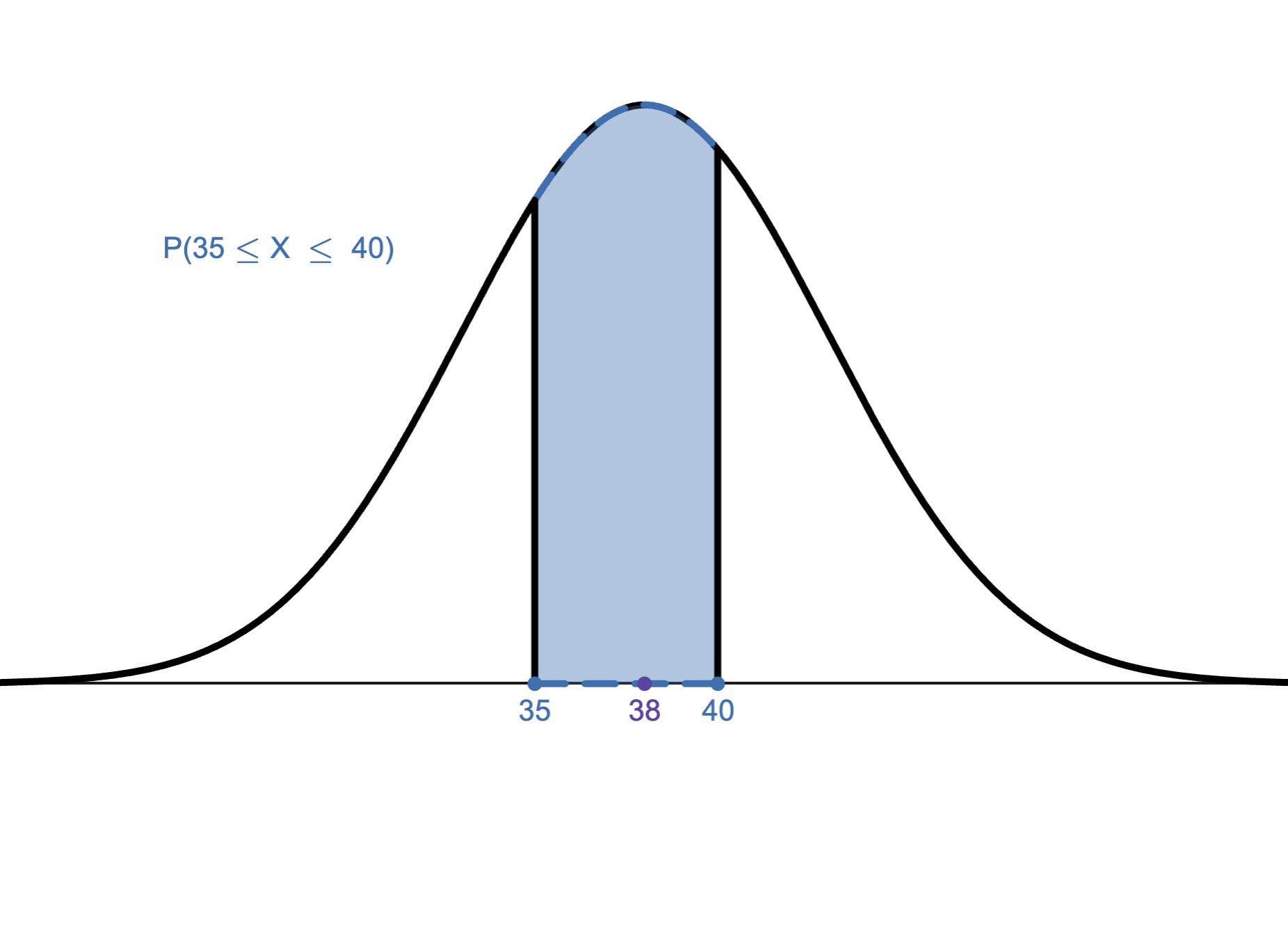
What formula would you use to find the probability shown below?
Options:
NORM.DIST(35,38,5,1)-NORM.DIST(40,38,5,1)
NORM.DIST(40,38,5,1)-NORM.DIST(35,38,5,1)
NORM.DIST(40,5,38,1)-NORM.DIST(35,5,38,1)
NORM.DIST(35,5,38,1)-NORM.DIST(40,5,38,1)
NORM.DIST(40,38,5,0)-NORM.DIST(35,38,5,0)
NORM.DIST(35,38,5,0)-NORM.DIST(40,38,5,0)
NORM.S.DIST(40,1)-NORM.S.DIST(35,1)